Introduzione. L’andamento del numero complessivo dei contagiati dall’inizio dell’epidemia di coronavirus è l’indicatore più immediato per seguire questo fenomeno, più del numero dei decessi, il quale dipende molto dal grado di letalità del virus e dall’efficienza del sistema sanitario di un paese.
Spesso, per seguire questo fenomeno si fa riferimento alla curva logistica, curva ben nota in letteratura, formata da un ramo esponenziale, con la concavità rivolta verso l’alto, seguita da un secondo ramo ad andamento logaritmico con la concavità verso il basso. Il momento in cui questa funzione modifica la sua curvatura è fondamentale, perché ci dice quando i tassi di contagio iniziano a ridursi fino ad annullarsi, e di conseguenza la curva dei contagi si avvia a divenire piatta.
La curva logistica è stata in passato utilizzata frequentemente dai demografi per descrivere la crescita di popolazioni, in quanto costituiva il superamento della legge maltusiana di crescita illimitata in assenza di vincoli esterni, come la limitatezza delle risorse. In estrema sintesi: in assenza di vincoli esterni, come appunto la limitatezza delle risorse alimentari, secondo l’approccio maltusiano, le popolazioni tenderebbero a crescere illimitatamente con una forza invariata nel tempo, cioè a un tasso costante. Ma il popolamento della Terra, come è noto, non è avvenuto con una forza invariabile, ma attraverso cicli caratterizzati da espansioni e contrazioni. Come è facile verificare, la legge di crescita maltusiana, mentre descrive bene l’evoluzione di breve periodo di una popolazione, nel lungo periodo porta a risultati paradossali. Infatti, la costanza del tasso di crescita che la caratterizza rappresenterebbe la sua pura capacità riproduttiva, in assenza di vincoli esterni, sia biologici che sociali. Nella realtà, invece, numerosi sarebbero gli “attriti” che farebbero e fanno sì che il tasso di crescita si allontani dal valore costante, particolarmente quando si considerino i grandi numeri.
Partendo da queste considerazioni nel passato si è cercata una legge descrittiva più raffinata che tenesse conto dei freni all’accrescimento illimitato di una popolazione. Nel 1825 il Quételet nel suo saggio Physique sociale aveva osservato che gli ostacoli all’aumento smisurato della popolazione crescono proporzionalmente al quadrato della velocità con cui la popolazione tende a crescere. Il Verhulst nel 1837 formalizzò nella curva logistica i concetti espressi dal Quételet, curva che venne poi riscoperta dagli studiosi americani Pearl e Reed nel 1920. La curva logistica si otterrebbe così correggendo il tasso di crescita maltusiana con un fattore, espressione degli “attriti”, che contrastando la crescita maltusiana della popolazione renderebbe il tasso reale sempre più piccolo fino ad azzerarlo.
Il modello logistico ha conosciuto in passato periodi di grande splendore: l’aderenza dei dati della popolazione americana a questo modello portò infatti a far credere che era stato trovato uno strumento molto preciso nel campo delle prospettive demografiche. Successive prove smentirono però questi primi risultati incoraggianti e considerazioni approfondite sulla struttura di questo modello ne misero in evidenza i limiti perché è irrealistico pensare che l’evoluzione della popolazione umana possa essere misurata da una funzione come quella logistica che dipende da pochi parametri. Al contrario, la logistica funzionerebbe bene per popolazioni di batteri e virus, campo in cui trova utili e feconde applicazioni.
L’andamento dei contagi in Calabria. Quanto detto in precedenza si adatta, dunque, perfettamente alla descrizione del COVID-19, sostituendo al termine “popolazione” quello dei “contagiati”. Di conseguenza, l’analisi del suo trend è molto utile, come si sta facendo oggi, per capire se la forma della curva dei contagi, ancora oggi di forma esponenziale, stia per cambiare nel profilo logaritmico. In questa nota anche noi abbiamo fatto questo esercizio, che dà una ulteriore conferma che in Calabria non si è ancora giunti al tanto atteso punto di break, come risulta dall’evoluzione dei contagi riportati in Figura 1, valori che sono ben interpolati da un polinomio di secondo grado (indice di determinazione R2= 0,9889).
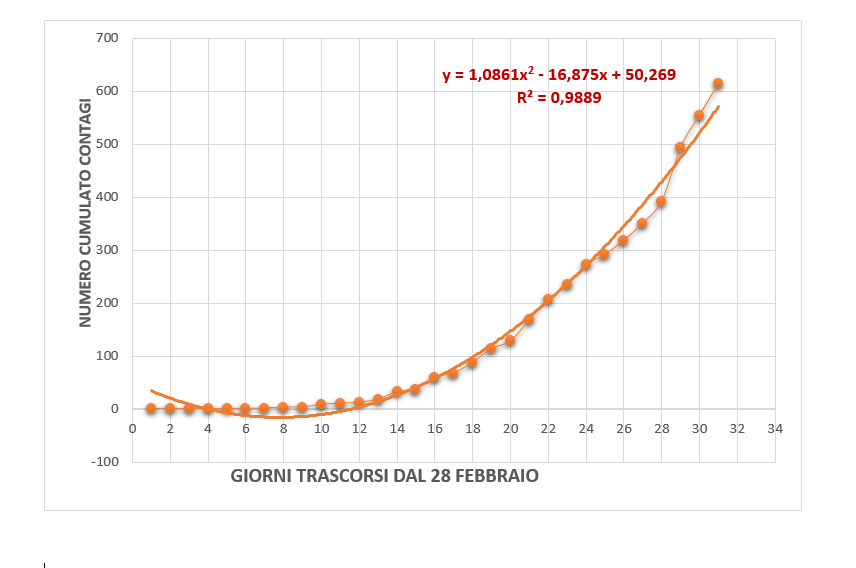
Tuttavia, osserviamo che le stime dei tassi istantanei di contagio, da noi calcolati sulla serie a partire dal nono giorno, Figura 2, mostrano chiaramente che è in atto una decisa tendenza alla riduzione, e ciò fa ben sperare che in tempi ragionevoli l’epidemia possa, se le misure attuali saranno mantenute, imboccare il tracciato della curva logistica che porterà al tanto atteso “plateau” del numero dei contagi.

Referenze
- P.F. Verhulst, Recherches mathématiques sur la loi d’accroissement de la population, Nouveaux memoires de l’Académie Royale, Bruxelles, 1845
- Aiello, Coronavirus in Italia: riapriamo il paese? No, è ancora troppo presto, www.opencalabria.com, 29-03-2020
- V.M.R. Muggeo, M. Porcu, La curva dei contagiati da COVID-19: la ricerca del punto di svolta, www.neodemos.info , 17-03-2020 https://lab.gedidigital.it/gedi-visual/2020/coronavirus-in-italia/















